2020年甘肃省陇南市中考数学真题及答案.doc-资料库

第1页 / 共21页

第2页 / 共21页

第3页 / 共21页

第4页 / 共21页

第5页 / 共21页

第6页 / 共21页

第7页 / 共21页

第8页 / 共21页

2020 年甘肃省陇南市中考数学真题及答案（考试时间 120 分钟，满分 120 分）一、选择题：本大题共 10 小题，每小题 3 分，共 30 分，每小题只有一个正确选项． 1．下列实数是无理数的是（） A．﹣2 B． C． D． 2．若α＝70°，则α的补角的度数是（） A．130° B．110° C．30° D．20° 3．若一个正方形的面积是 12，则它的边长是（） A．2 B．3 C．3 D．4 4．下列几何体中，其俯视图与主视图完全相同的是（） A． B． C． D． 5．下列各式中计算结果为 x6 的是（） A．x2+x4 B．x8﹣x2 C．x2•x4 D．x12÷x2 6．生活中到处可见黄金分割的美．如图，在设计人体雕像时，使雕像的腰部以下 a 与全身 b 的高度比值接近 0.618，可以增加视觉美感．若图中 b 为 2 米，则 a 约为（） A．1.24 米 B．1.38 米 C．1.42 米 D．1.62 米 7．已知 x＝1 是一元二次方程（m﹣2）x2+4x﹣m2＝0 的一个根，则 m 的值为（） A．﹣1 或 2 B．﹣1 C．2 D．0 8．如图所示的木制活动衣帽架是由三个全等的菱形构成，根据实际需要可以调节 AE 间的距离．若 AE 间的距离调节到 60cm，菱形的边长 AB＝20cm，则∠DAB 的度数是（）

A．90° B．100° C．120° D．150° 9．如图，A 是⊙O 上一点，BC 是直径，AC＝2，AB＝4，点 D 在⊙O 上且平分，则 DC 的长为（） A．2 B． C．2 D． 10．如图①，正方形 ABCD 中，AC，BD 相交于点 O，E 是 OD 的中点．动点 P 从点 E 出发，沿着 E→O→B→A 的路径以每秒 1 个单位长度的速度运动到点 A，在此过程中线段 AP 的长度 y 随着运动时间 x 的函数关系如图②所示，则 AB 的长为（） A．4 B．4 C．3 D．2 二、填空题：本大题共 8 小题，每小题 3 分，共 24 分． 11．如果盈利 100 元记作+100 元，那么亏损 50 元记作元． 12．分解因式：a2+a＝． 13．暑假期间，亮视眼镜店开展学生配镜优惠活动．某款式眼镜的广告如下，请你为广告牌填上原价．原价：元暑假八折优惠，现价：160 元 14．要使分式有意义，x 需满足的条件是． 15．在一个不透明的袋中装有若干个材质、大小完全相同的红球，小明在袋中放入 3 个黑球（每个黑球除颜色外其余都与红球相同），摇匀后每次随机从袋中摸出一个球，记录颜色后放回袋中，通过大量重复摸球试验后发现，摸到红球的频率稳定在 0.85 左右，估计袋中红球有个． 16．如图，在平面直角坐标系中，△OAB 的顶点 A，B 的坐标分别为（3，），（4，0）．把 △ OAB 沿 x 轴向右平移得到 △ CDE ，如果点 D 的坐标为（ 6 ，），则点 E 的坐标

为． 17．若一个扇形的圆心角为 60°，面积为 cm2，则这个扇形的弧长为 cm（结果保留π）． 18．已知 y＝ ﹣x+5，当 x 分别取 1，2，3，…，2020 时，所对应 y 值的总和是．三、解答题（一）：本大题共 5 小题，共 26 分．解答应写出必要的文字说明，证明过程或演算步骤． 19．（4 分）计算：（2﹣ ）（2+ ）+tan60°﹣（π﹣2 ）0． 20．（4 分）解不等式组：，并把它的解集在数轴上表示出来． 21．（6 分）如图，在△ABC 中，D 是 BC 边上一点，且 BD＝BA．（1）尺规作图（保留作图痕迹，不写作法）： ①作∠ABC 的角平分线交 AD 于点 E； ②作线段 DC 的垂直平分线交 DC 于点 F．（2）连接 EF，直接写出线段 EF 和 AC 的数量关系及位置关系． 22．（6 分）图①是甘肃省博物馆的镇馆之宝﹣﹣铜奔马，又称“马踏飞燕”，于 1969 年 10 月出土于武威市的雷台汉墓，1983 年 10 月被国家旅游局确定为中国旅游标志．在很多旅游城市的广场上都有“马踏飞燕”雕塑．某学习小组把测量本城市广场的“马踏飞燕” 雕塑（图②）最高点离地面的高度作为一次课题活动，同学们制定了测量方案，并完成了实地测量，测得结果如下表：课题测量“马踏飞燕“雕塑最高点离地面的高度

如图，雕塑的最高点 B 到地面的高度为 BA，在测点 C 用仪器测得点 B 的仰角为α，前进一段距离到达测点 E，再用该仪器测得点 B 的仰角为β，且点 A，B，C，D，E，F 均在同一竖直平面内，点 A，C，E 在同一条直线上． α的度数 β的度数 CE 的长度仪器 CD（EF）的高度 31° 42° 5 米 1.5 米测量示意图测量数据请你根据上表中的测量数据，帮助该小组求出“马踏飞燕”雕塑最高点离地面的高度（结果保留一位小数）．（参考数据：sin31°≈0.52，cos31°≈0.86，tan31°≈0.60，sin42° ≈0.67，cos42°≈0.74，tan42°≈0.90） 23．（6 分）2019 年甘肃在国际知名旅游指南《孤独星球》亚洲最佳旅游地排名第一．截至 2020 年 1 月，甘肃省已有五家国家 5A 级旅游景区，分别为 A：嘉峪关文物景区；B：平凉崆峒山风景名胜区；C：天水麦积山景区；D：敦煌鸣沙山月牙泉景区；E：张掖七彩丹霞景区．张帆同学与父母计划在暑假期间从中选择部分景区游玩．（1）张帆一家选择 E：张掖七彩丹霞景区的概率是多少？（2）若张帆一家选择了 E：张掖七彩丹霞景区，他们再从 A，B，C，D 四个景区中任选两个景区去旅游，求选择 A，D 两个景区的概率（要求画树状图或列表求概率）．四、解答题（二）：本大题共 5 小题，共 40 分．解答应写出必要的文字说明，证明过程或演算步骤． 24．（7 分）习近平总书记于 2019 年 8 月在兰州考察时说“黄河之滨也很美”．兰州是古丝绸之路商贸重镇，也是黄河唯一穿城而过的省会城市，被称为“黄河之都”．近年来，在市政府的积极治理下，兰州的空气质量得到极大改善，“兰州蓝”成为兰州市民引以为豪的城市名片．如图是根据兰州市环境保护局公布的 2013～2019 年各年的全年空气质量优良天数绘制的折线统计图．

请结合统计图解答下列问题：（1）2019 年比 2013 年的全年空气质量优良天数增加了天；（2）这七年的全年空气质量优良天数的中位数是天；（3）求这七年的全年空气质量优良天数的平均天数；（4）《兰州市“十三五”质量发展规划》中指出：2020 年，确保兰州市全年空气质量优良天数比率达 80%以上．试计算 2020 年（共 366 天）兰州市空气质量优良天数至少需要多少天才能达标． 25．（7 分）通过课本上对函数的学习，我们积累了一定的经验．下表是一个函数的自变量 x 与函数值 y 的部分对应值，请你借鉴以往学习函数的经验，探究下列问题： x y … … 0 6 1 3 2 2 3 4 1.5 1.2 5 1 … … （1）当 x＝时，y＝1.5；（2）根据表中数值描点（x，y），并画出函数图象；（3）观察画出的图象，写出这个函数的一条性质：． 26．（8 分）如图，⊙O 是△ABC 的外接圆，其切线 AE 与直径 BD 的延长线相交于点 E，且 AE ＝AB．（1）求∠ACB 的度数；（2）若 DE＝2，求⊙O 的半径．

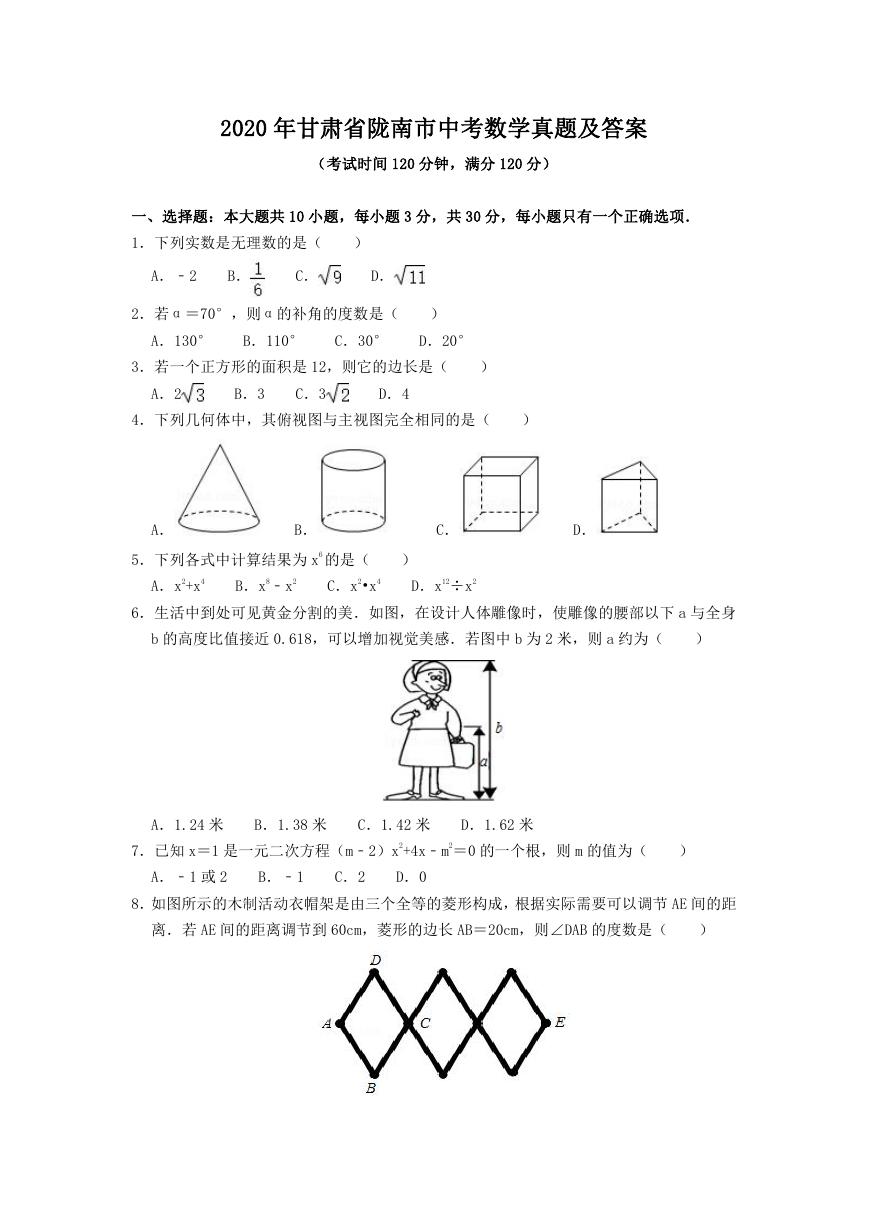
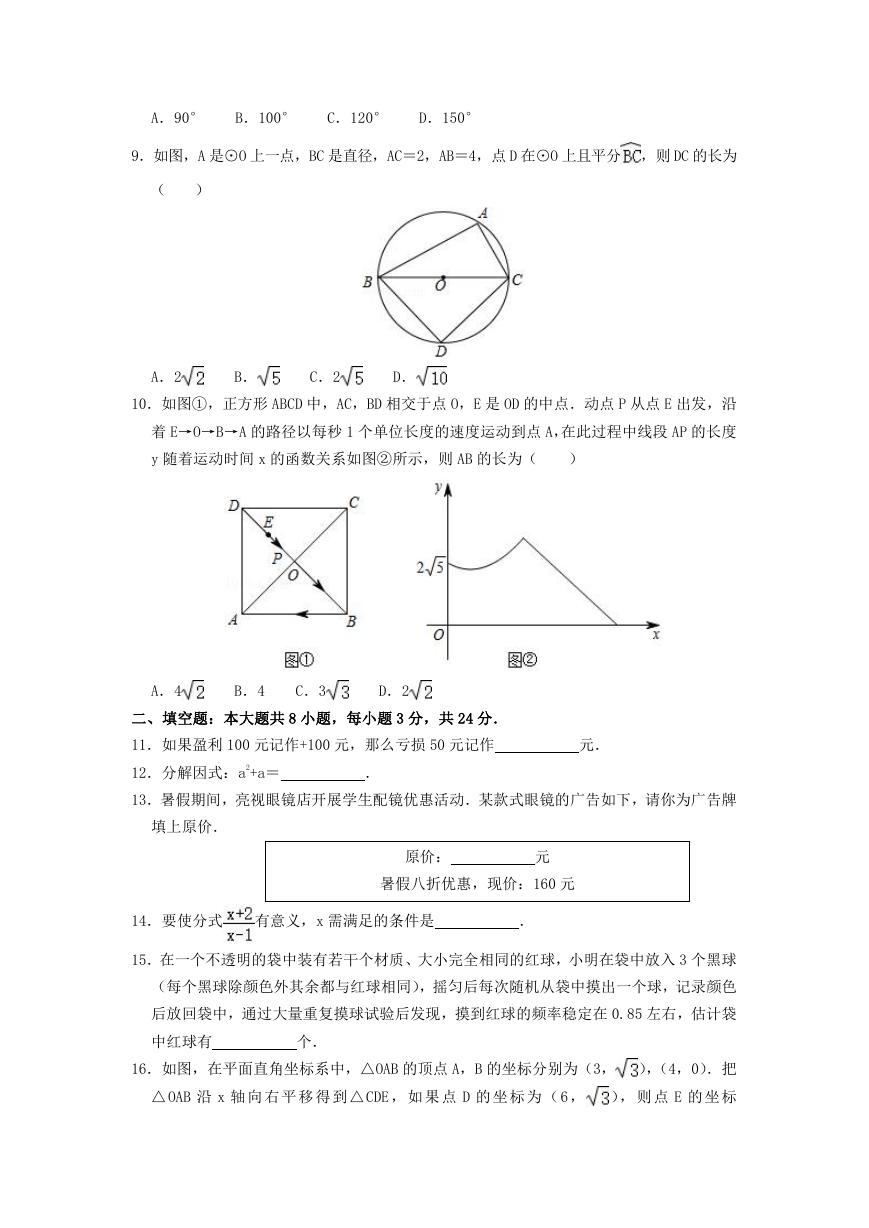
27．（8 分）如图，点 M，N 分别在正方形 ABCD 的边 BC，CD 上，且∠MAN＝45°．把△ADN 绕点 A 顺时针旋转 90°得到△ABE．（1）求证：△AEM≌△ANM．（2）若 BM＝3，DN＝2，求正方形 ABCD 的边长． 28．（10 分）如图，在平面直角坐标系中，抛物线 y＝ax2+bx﹣2 交 x 轴于 A，B 两点，交 y 轴于点 C，且 OA＝2OC＝8OB．点 P 是第三象限内抛物线上的一动点．（1）求此抛物线的表达式；（2）若 PC∥AB，求点 P 的坐标；（3）连接 AC，求△PAC 面积的最大值及此时点 P 的坐标．参考答案与解析一、选择题：本大题共 10 小题，每小题 3 分，共 30 分，每小题只有一个正确选项．

1．下列实数是无理数的是（） A．﹣2 B． C． D．【知识考点】算术平方根；无理数．【思路分析】根据无理数的定义（无理数是指无限不循环小数）逐个判断即可．【解题过程】解：＝3，则由无理数的定义可知，属于无理数的是．故选：D． 2．若α＝70°，则α的补角的度数是（） A．130° B．110° C．30° D．20° 【知识考点】余角和补角．【思路分析】根据补角的定义，两个角的和是 180°即可求解．【解题过程】解：α的补角是：180°﹣∠A＝180°﹣70°＝110°．故选：B． 3．若一个正方形的面积是 12，则它的边长是（） A．2 B．3 C．3 D．4 【知识考点】算术平方根．【思路分析】根据算术平方根的定义解答．【解题过程】解：∵正方形的面积是 12， ∴它的边长是＝2 ．故选：A．【总结归纳】本题考查了算术平方根，解题的关键是利用了正方形的性质和算术平方根的定义． 4．下列几何体中，其俯视图与主视图完全相同的是（） A． B． C． D．【知识考点】简单几何体的三视图．【思路分析】根据圆锥、圆柱、正方体、三棱柱的主视图、俯视图矩形判断即可．【解题过程】解：圆锥的主视图是等腰三角形，俯视图是圆，因此 A 不符合题意；圆柱的主视图是矩形，俯视图是圆，因此 B 不符合题意；正方体的主视图、俯视图都是正方形，因此选项 C 符合题意；三棱柱的主视图是矩形，俯视图是三角形，因此 D 不符合题意；故选：C． 5．下列各式中计算结果为 x6 的是（） A．x2+x4 B．x8﹣x2 C．x2•x4 D．x12÷x2

【知识考点】合并同类项；同底数幂的乘法；同底数幂的除法．【思路分析】根据合并同类项、同底数幂乘除法的性质进行计算即可．【解题过程】解：x2 与 x4 不是同类项，不能合并计算，它是一个多项式，因此 A 选项不符合题意；同理选项 B 不符合题意； x2•x4＝x2+4＝x6，因此选项 C 符合题意； x12÷x2＝x12﹣2＝x10，因此选项 D 不符合题意；故选：C． 6．生活中到处可见黄金分割的美．如图，在设计人体雕像时，使雕像的腰部以下 a 与全身 b 的高度比值接近 0.618，可以增加视觉美感．若图中 b 为 2 米，则 a 约为（） A．1.24 米 B．1.38 米 C．1.42 米 D．1.62 米【知识考点】黄金分割．【思路分析】根据雕像的腰部以下 a 与全身 b 的高度比值接近 0.618，因为图中 b 为 2 米，即可求出 a 的值．【解题过程】解：∵雕像的腰部以下 a 与全身 b 的高度比值接近 0.618， ∴ ≈0.618， ∵b 为 2 米， ∴a 约为 1.24 米．故选：A． 7．已知 x＝1 是一元二次方程（m﹣2）x2+4x﹣m2＝0 的一个根，则 m 的值为（） A．﹣1 或 2 B．﹣1 C．2 D．0 【知识考点】一元二次方程的定义；一元二次方程的解．【思路分析】首先把 x＝1 代入（m﹣2）x2+4x﹣m2＝0 解方程可得 m1＝2，m2＝﹣1，再结合一元二次方程定义可得 m 的值．【解题过程】解：把 x＝1 代入（m﹣2）x2+4x﹣m2＝0 得： m﹣2+4﹣m2＝0， ﹣m2+m+2＝0，解得：m1＝2，m2＝﹣1， ∵（m﹣2）x2+4x﹣m2＝0 是一元二次方程， ∴m﹣2≠0，

资料库

2020年甘肃省陇南市中考数学真题及答案.doc

相关推荐

中考

热门标签

最新资料